Funding Phase II
To answer those questions, project B01 focuses on the characterisation and modelling of adaptive structures. Furthermore, methods for model order reduction are applied and extended on the custom requirements of adaptive structures.
Methods for design, mechanical modelling, analysis and optimisation of structures are inherently connected to the understanding of the mechanical behaviour of load bearing structures in engineering. Considering ultra-lightweight adaptive structures, this understanding has to be extended to smart and active reactions to external influences. In order to characterise the mechanical behaviour of adaptive structures, stability, static determinacy, stiffness, strength, and ductility are important characteristics. Those can be investigated considering a material point, a cross section (for truss and beam structures), or a whole structure.
Photo: (c) ILEK
A main objective of B01 is the development of methods to identify the most important and desirable capabilities of well-designed adaptive structures, to learn how such a structure can be designed, and how such information can be provided to the control. The adaptive structure is defined as a new archetype of structures. This facilitates an integral design of adaptive structures, as opposed to adding adaptive components to an initial design of a passive structure.
To enable simulation of adaptive structures, the global model including variable actuator placements should be appropriate for model order reduction. The numerical effort for dynamic simulations (especially in real-time) or optimisation of adaptive structures is huge. Due to that fact, model order reduction plays an important role in this project.
In the first period of the project, answers to the following questions were found:
- How can adaptive structures be characterised?
- Which criteria and characteristics are relevant and desirable for an adaptive structure?
- How can adaptive structures be modelled and analysed?
- Which methods for model order reduction can be applied onto models with variable actuator placements?
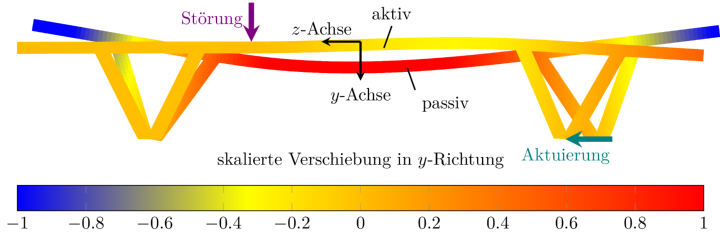
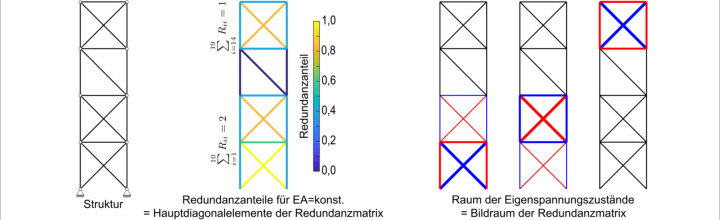
Research was done on possible types of actuator modelling. A beam actuator element that is suitable for modelling adaptive truss structures was presented. The redundancy matrix, which allows an analysis of truss structures from a structural point of view, and control engineering methods based on gramian matrices were used to characterise adaptive structures and for optimal actuator placement. Similarities and differences between those methods were identified.
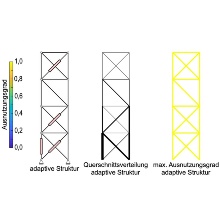
Results for the redundancy distribution of a plane truss with equal cross sectional area in all elements. The degree of statical indeterminacy of the assembly equals three.
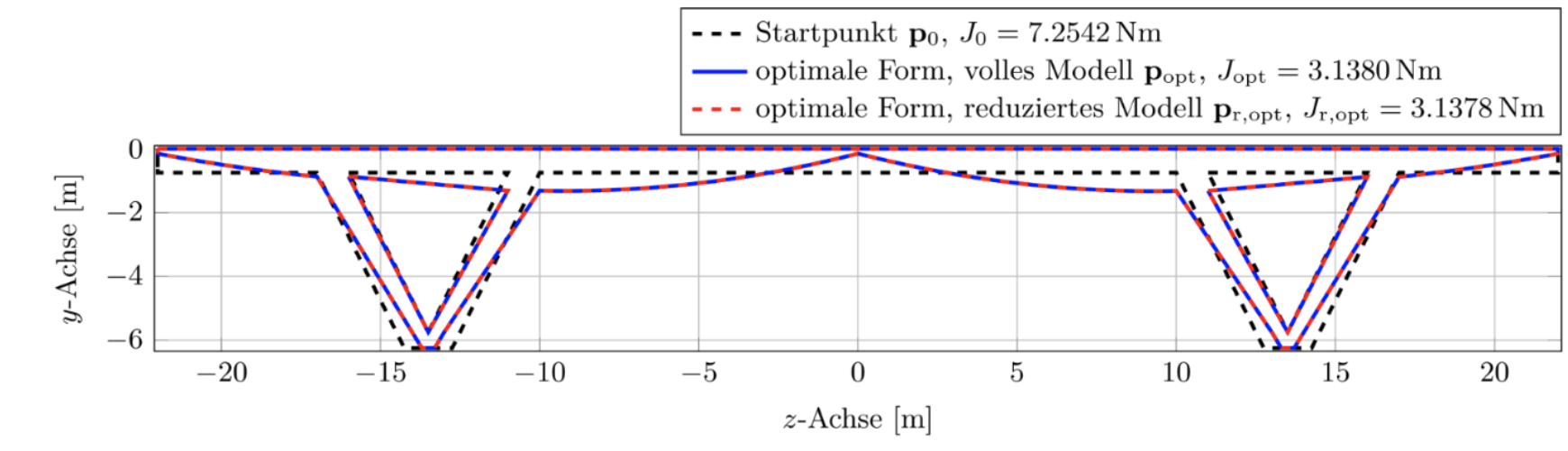
Furthermore, a method was developed to specify the system matrices as a function of geometry parameters in an analytical and affine representation. With interpolation-based reduction methods, the number of degrees of freedom of the system was significantly reduced, while the affine parameter dependency in the reduced system matrices was preserved, which enabled a numerically efficient evaluation of the parameterised system.
Shape optimization results for an adaptive structure, calculated with a full and a parametric reduced model Photo: ITM
In the further phase of the project, the focus will be on extending the previous work with regard to different structural topologies and their suitability for adaptation, as well as the extension of the methods to include shell structures. The research questions can be formulated as follows:
- How can the redundancy concept be applied to planar structures?
- How must the redundancy concept be extended to be applicable to nonlinear and dynamical systems?
- How can shell structures be modelled considering different actuators?
- How can parametric model reduction methods be applied to adaptive shell structures?
- How can modular structural components be parametrically reduced?
- How can these methods be used in topology optimisation?
Project B01 provides information on (reduced) modelling and characterisation as an important prerequisite of many other projects of the collaborative research centre.
Subproject Leader
- Prof. Dr.-Ing. habil. Manfred Bischoff, Institute for Structural Mechanics
- Prof. Dr.-Ing. habil. Prof. E. h. Peter Eberhard, Institute of Engineering and Computational Mechanics
Funding Phase I
To answer those questions, project B01 focuses on the characterisation and modelling of adaptive structures. Furthermore, methods for model order reduction are applied and extended on the custom requirements of adaptive structures.
Methods for design, mechanical modelling, analysis and optimisation of structures are inherently connected to the understanding of the mechanical behaviour of load bearing structures in engineering. Considering ultra-lightweight adaptive structures, this understanding has to be extended to smart and active reactions to external influences. In order to characterise the mechanical behaviour of adaptive structures, stability, static determinacy, stiffness, strength, and ductility are important characteristics. Those can be investigated considering a material point, a cross section (for truss and beam structures), or a whole structure.
A main objective of B01 is the development of methods to identify the most important and desirable capabilities of well-designed adaptive structures, to learn how such a structure can be designed, and how such information can be provided to the control. The adaptive structure is defined as a new archetype of structures. This facilitates an integral design of adaptive structures, as opposed to adding adaptive components to an initial design of a passive structure.
Following the objectives of the project, the following questions arise:
- How can adaptive structures be characterised?
- Which criteria and characteristics are relevant and desirable for an adaptive structure?
- How can adaptive structures be modelled and analysed?
- Which methods for model order reduction can be applied onto models with variable actuator placements?
The focus of project B01 is set on the modelling and the simulation of adaptive structures. Because of its large influence on the design process, the actuation should be included in an early stage. The objective is to define simple but accurate models of actuators in order to represent the actuation in the simulations. In this context, the finite element method is an important tool for static analyses, dynamic simulations and optimisation of structures.
To enable simulation of adaptive structures, the global model including variable actuator placements should be appropriate for model order reduction. The numerical effort for dynamic simulations (especially in real-time) or optimisation of adaptive structures is huge. Due to that fact, model order reduction plays an important role in this project. The objective is to extend existing methods and to implement the new developments at ITM into NumPro, the FEM-Code of IBB.
Based on modelling and simulation, a new structural typology should be defined as a characterising and describing tool for adaptive structures. This expands the existing structural classification by the actuation of load bearing structures.
Project B01 provides information on (reduced) modelling and characterisation as an important prerequisite of many other projects of the collaborative research centre.
Subproject Leader
- Prof. Dr.-Ing. habil. Manfred Bischoff, Institute for Structural Mechanics
- Prof. Dr.-Ing. habil. Prof. E. h. Peter Eberhard, Institute of Engineering and Computational Mechanics
Publications
- J. Gade, F. Geiger, R. Kemmler, and M. Bischoff, “A form-finding method for adaptive truss structures subject to multiple static load cases,” International Journal of Space Structures, Jan. 2024, doi: 10.1177/09560599231212707.
- M. Vierneisel, F. Geiger, M. Bischoff, and P. Eberhard, “Derivation of Geometrically Parameterized Shell Elements in the Context of Shape Optimization,” presented at the Symposium on Optimal Design and Control of Multibody Systems - Adjoint Methods, Alternatives, and Beyond, and, Ed., 2024. doi: https://doi.org/10.1007/978-3-031-50000-8_6.
- A. Trautwein, T. Prokosch, G. Senatore, L. Blandini, and M. Bischoff, “Analytical and numerical case studies on tailoring stiffness for the design of structures with displacement control,” Frontiers in Build Environment, pp. 1–14, May 2023, doi: https://doi.org/10.3389/fbuil.2023.1135117.
- M. Vierneisel, A. Zeller, S. Dakova, M. Böhm, O. Sawodny, and P. Eberhard, “PARAMETRIC MODEL ORDER REDUCTION FOR PARAMETER IDENTIFICATION OF ADAPTIVE HIGH-RISE STRUCTURES,” in 10th ECCOMAS Thematic Conference on Smart Structures and Materials, in 10th ECCOMAS Thematic Conference on Smart Structures and Materials. Dept. of Mechanical Engineering & Aeronautics University of Patras, 2023. doi: 10.7712/150123.9820.443871.
- L.-M. Krauss, M. Von Scheven, and M. Bischoff, “COMBINING THE REDUNDANCY CONCEPT AND VIBRATION CONTROL FOR ACTUATOR PLACEMENT IN ADAPTIVE STRUCTURES,” in 10th ECCOMAS Thematic Conference on Smart Structures and Materials, in 10th ECCOMAS Thematic Conference on Smart Structures and Materials. Dept. of Mechanical Engineering & Aeronautics University of Patras, 2023, pp. 723–734. doi: 10.7712/150123.9826.444394.
- A. Trautwein, T. Prokosch, and M. Bischoff, “A CASE STUDY ON TAILORING STIFFNESS FOR THE DESIGN OF ADAPTIVE RIB-STIFFENED SLABS,” in 10th ECCOMAS Thematic Conference on Smart Structures and Materials, in 10th ECCOMAS Thematic Conference on Smart Structures and Materials. Dept. of Mechanical Engineering & Aeronautics University of Patras, 2023. doi: 10.7712/150123.9821.444802.
- T. Prokosch, J. Stiefelmaier, C. Tarın, and M. Bischoff, “DETECTION AND IDENTIFICATION OF STRUCTURAL FAILURE USING THE REDUNDANCY MATRIX,” in 10th ECCOMAS Thematic Conference on Smart Structures and Materials, in 10th ECCOMAS Thematic Conference on Smart Structures and Materials. Dept. of Mechanical Engineering & Aeronautics University of Patras, 2023. doi: 10.7712/150123.9827.444431.
- M. Böhm et al., “Input modeling for active structural elements – extending the established FE-Workflow for modeling of adaptive structures,” in IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), in IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). Jul. 2020, pp. 1595--1600. doi: 10.1109/AIM43001.2020.9158996.
- F. Geiger, J. Gade, M. von Scheven, and M. Bischoff, “Optimal Design of Adaptive Structures vs. Optimal Adaption of Structural Design,” in IFAC-PapersOnLine, in IFAC-PapersOnLine, vol. 53. IFAC World Congress 2020, 11.-17.07.2020, Berlin, Germany, 2020, pp. 8363--8369. doi: 10.1016/j.ifacol.2020.12.1604.
- F. Geiger, J. Gade, M. von Scheven, and M. Bischoff, “A Case Study on Design and Optimization of Adaptive Civil Structures,” Frontiers in Built Environment, vol. 6, Jul. 2020, doi: 10.3389/fbuil.2020.00094.
- B. Fröhlich, J. Gade, F. Geiger, M. Bischoff, and P. Eberhard, “Geometric element parameterization and parametric model order reduction in finite element based shape optimization,” Computational Mechanics, vol. 63, pp. 853–868, 2019, doi: 10.1007/s00466-018-1626-1.
- N. Walker and P. Eberhard, “Model Order Reduction of a Modular Scale Model of a High Rise Building,” 2019, doi: 10.1002/pamm.201900069.
- B. Fröhlich, F. Geiger, J. Gade, M. Bischoff, and P. Eberhard, “Model order reduction of coupled, parameterized elastic bodies for shape optimization,” in IUTAM Symposium on Model Order Reduction of Coupled Systems, May 22–25, 2018, Stuttgart, in IUTAM Symposium on Model Order Reduction of Coupled Systems, May 22–25, 2018, Stuttgart. 2018, pp. 151--163. doi: 10.1007/978-3-030-21013-7_11.
- J. L. Wagner et al., “On steady-state disturbance compensability for actuator placement in adaptive structures,” at – Automatisierungstechnik, vol. 66, pp. 591–603, 2018, doi: 10.1515/auto-2017-0099.
- J. Gade, R. Kemmler, M. Drass, and J. Schneider, “Enhancement of a meso-scale material model for nonlinear elastic finite element computations of plain-woven fabric membrane structures,” Engineering Structures, vol. 177, pp. 668–681, 2018, doi: 10.1016/j.engstruct.2018.04.039.
Ansprechpersonen
Manuel Vierneisel
M.Sc.Doctoral Researcher
Lisa-Marie Krauß
M. Sc.Doctoral Researcher
Tamara Prokosch
M. Sc.Doctoral Researcher